A game approach to the Crimean crisis. Part I: Game Description

Game theory can say something non-trivial about any strategic interaction, and separatism movements are by no means an exception. In the following, I model the strife between Russian and Ukrainian governments over the Crimean Republic and Sevastopol as an extensive game with simultaneous moves which may supply us with verifiable predictions about equilibrium strategies of the players and their outcomes.

Players

It has become a truism to say that international relations (and politics in general) are a result of actions of many agents, many of whom are not perfectly rational. Although it is somewhat a fair description of interactions in domestic politics (at least when it comes to the multiplicity of players and their interests), conflicts between states involve much fewer people with significant marginal impact because resources (first of all, the army) are (i) detached from the citizens and (ii) centralized (that is, managed by a single person such as the president) to a qualitatively greater extent. Thus, reducing the set of players to a handful of politicians is without loss of generality and ensures tractability.

The full set of players should include the Crimean Republic, Sevastopol, Russia, Ukraine, the EU bureaucracy, Germany, Poland and several other European states, and the US. Though realistic, including all countries’ leaders in the game makes the solution finding too a complex endeavor. Therefore, I shall only consider three agents here: the Russian president, the Ukrainian government and the Crimean and Sevastopol population. Choosing to represent Crimea as a collective agent consisting of its population rather than its government emphasizes the fact that the latter has not yet acquired authority such as taxation or armed forces. At the same time, locals will be deciding the referendum outcome which is bound to play a crucial role in the conflict.

Modeling a collective player could seem tricky at first. Instead of representing each citizen as a single player, we can distinguish between different types of citizens and then use their proportions as probabilities that this type realizes. Here, it is sufficient to distinguish between pro-Russian and pro-Ukrainian types of voters, and to note that the proportion of the former type is higher. To be consistent with the literature, let Θ denote the set of types. Therefore, Θ = {θ_R, θ_U} such that Pr(θ_R) > Pr(θ_U). Why is probability equivalent to proportions? Because if you randomly draw one person from the population, the probability that she is of type θ is precisely the same that the share of type θ in the population.

Strategies

A strategy is a full combination of actions available to a player. For simplicity, I assume that both governments choose actions along two independent dimensions: financial and military. The financial decision shows how much aid the government, Ukrainian or Russian, is offering to the citizens in Crimea which they receive as wages, social entitlements, infrastructural projects or even one-shot payments. The military decision is more straightforward and involves the amount of armed forces used in the conflict. To avoid complexities, I do not distinguish between the qualitative side of the military decision such as direct or indirect involvement of troops or the type of armed forces used. This distinction may turn out to be important, but for the sake of tractability the decision is assumed to be just about more and less troops.

The continuum of transfers and military is bounded from below (at zero) and from above. The upper boundary is specific for each country and is determined by exogenous factors such as GDP, institutional design and so on. Importantly, both upper boundaries are higher for Russia so it is assumed to be capable of spending more on aid and to send more armed forces. By denoting the upper limit by L_gd, where g = R, U stands for government and d = F, M for dimension we obtain F_g = [0, L_gF] and M_g = [0, L_gM] such that L_Rd > L_Ud, for all d in D. Consequently, the set of strategies available for each g is the Cartesian product S_g = F_g × M_g, i.e. we speak of strategies as of ordered pairs like (f_g, m_g) showing feasible combinations of actions in both dimensions.

Finally, Crimean citizens face a binary choice whether to vote for staying in Ukraine or joining Russia. Although real ballots will have two yes/no questions plus the option to abstain which makes it five strategies in total, the actual choice is between two countries, so restricting the strategy set is without loss of generality. Now recall that Crimea is modeled as a collective yet single actor whose strategy is the choice of the majority. By assumption, the majority of voters are pro-Russian, so this type includes the median voter who determines the outcome, and we could thus neglect the other type. Formally, the Crimean Republic chooses from S_C = {U; R}. In more nuanced versions of this game one could assume a continuous distribution of voter types or that the exact percentage of votes matters, but I omit both intentionally as additional complexity or realism is neither sufficient nor necessary to improve the accuracy of predictions.

Utility functions and pay-offs

In line with public choice literature, politicians are treated as rent-seekers, meaning that they choose a strategy which maximizes their rents rather than social welfare. A reliable proxy for rents extracted by the Russian president could be his approval rating because a higher approval rate means higher tolerance for backroom deals and unjustified public spending as well as higher chances of re-election. As currently the Ukrainian government is facing problems of a different order, its leaders are motivated by the desire to stay in power, so their objective is to maximize the probability of winning presidency in Mai. And as to the Crimean voters, their interest lies in maximizing local public spending they expect to enjoy, but the types differ along the cultural dimension so the issue of belonging to another state matters in its own right.

I begin with the utility function of Crimean voters. They are assumed to care about following things:

• financial in-flows: the more aid from Russia and the more budget transfers from Kiev, the better. Utility increases with decreasing marginal returns
• cultural ‘premium’: voters have additional utility from living in a country they identify themselves with more closely (so-called linguistic, historic etc. ‘identity’)
• military intervention: voters dislike occupation from either state, but their disliking is less pronounced when the occupants come from the country they identify themselves more closely (utility losses from occupation have a decreasing marginal rate).

To formalize these ideas, let U_c denote the utility of voters. Recall that the strategy is determined by the majority of voters, that is, by the pro-Russian type. Therefore, it is sufficient to analyze under which conditions they will prefer the ‘exit’ option. They do this, of course, if and only if exit promises larger utility than staying in, U_c® ≥ U_c(U). Precisely, their utility from exit is

1. U_c® = f(F_R) + B_R – g(M_U, θ_R) – g(M_R, θ_R), where B denotes the ‘cultural premium’, f(·) is utility from financial inflows and g(·) disutility from military occupation. Furthermore, ∂U_c/∂F_g> 0, ∂²U_c/∂F_g² < 0, ∂U_c/∂M_g < 0 and ∂²U_c/∂M_g² > 0.

Similarly, their satisfaction from staying in Ukraine is

2. U_c(U) = f(F_U) – g(M_U, θ_R) – g(M_R, θ_R)

As dissatisfaction with occupation terms is identical in both cases (voters can not influence intervention), the scale of military involvement is irrelevant when determining the best response. What they are only able to influence is the source of budget transfers and the cultural closeness bonus. Let us rewrite the original inequality by substituting (1) and (2) in it and cancelling disutility terms on both sides out:

3. s_c^* = {R} if and only if f(F_R) + B_R ≥  f(F_U)

In a special case of purely materialistic voters when B_R  = 0, (3) simplifies to

4. s_c^* = {R} if and only if F_R ≥ F_U

So we have obtained an inequality that fully describes the referendum outcome. The majority votes to stay in Ukraine only if Kiev promises budget transfers that are not only higher than those offered by the Kremlin, but also cover pro-Russian voters’ opportunity costs of living in a country they feel more distant with. The simplicity of this best response function is helpful not only in its own right, but also for the sake of finding an equilibrium, because, as I show below, the other two utility functions are continuous and harder to deal with.

To model utility of the Russian president, first consider some intuition:

• giving aid to the Crimean Republic reduces spending available for Russian voters, so more aid decreases approval rating at an increasing rate, ceteris paribus
• starting military action when the opponent does not decreases approval rating at an increasing rate (treated as aggression)
• starting military action as a simultaneous response to the opponent’s military action increases approval rating (treated as defense) if the response is viewed adequate and sufficient to enhance victory.
• if the military response is too weak (not sufficient for victory) or too harsh (such as dropping a nuclear bomb as a response to gun-shooting), the approval rating drops.
• any military action incurs costs via sanctions imposed by Western states such that sanctions increase as intervention becomes more intensive. In turn, sanctions hurt Russian citizens, thereby increasingly decreasing the incumbent’s approval rating, all else equal. When Russia is treated as an aggressor, sanctions are harsher than when a defender.
• if the Crimean Republic and Sevastopol join Russia as their regions, the approval rating increases, ceteris paribus.

To formalize the essentials of this intuition, let U_R denote the Russian incumbent’s utility and let it be a function of chosen levels on two dimensions, both own and Ukraine’s, sanctions imposed, and the conflict outcome, U_R = U(F_R, F_U, M_R, M_U, V(S_C(F_R, F_U), M_R, M_U), P(M_R, M_U)), where P(·) denotes sanctions imposed and V(·) is the ‘victory function’ specifying which country gets the region. Moreover, ∂U/∂F_R < 0, ∂²U/∂F_R² < 0, ∂P(M_R, M_U))/∂M_R > 0, ∂²P(M_R, M_U))/∂M_R²> 0, ∂U/∂P(M_R, M_U))< 0 and ∂²U/∂P(M_R, M_U))² < 0. Verbally, Russia is facing interesting trade-offs because giving financial aid directly reduces approval ratings, but it can also increase them indirectly by ensuring Crimea’s joining. Similarly, using military force decreases approval rates indirectly via sanctions but it can increase them directly by conquering the region or being perceived as a ‘defender’ implementing an adequate response to the opponent’s aggression.

The above-specified conditions can be satisfied by the following utility function:

5. U_R =V(S_C(F_R, F_U), M_R, M_U) + A(M_R, M_U) – c(F_R) – P(M_R, M_U), where s(·) is the cost/benefit function of military action and c(·) denotes costs of financial aid

Further, the victory function models the conflict’s outcome such that Crimea belongs to the state which applies more military force, regardless of the referendum decision. In case the amount of military force applied is equal (meaningful at M_R= M_U = 0), the outcome is determined by the referendum,

The cost/benefit function of military action is quadratic with decreasing marginal returns when the state acts as a defender and strictly decreasing when an aggressor,

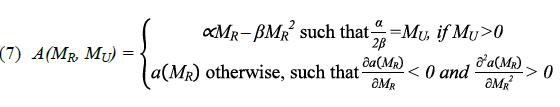
The assumption α/2β = M_U captures the idea that it is optimal to retaliate to the same extent that your opponent attacks, which is equivalent to the notion of “adequate response”. So, another interesting feature of this model is the fact that military action can be useful for its own sake even when it is not sufficient to win the territory, which could motivate politicians to apply force when it seems irrational.

Finally, Ukraine’s utility function is essentially a reduced version of (5). Namely, its government, being West-oriented and acting on its own territory, does not face the risk of sanctions in case it applies military force. Thus, it deals with the following program:

8. U_U =V(S_C(F_U, F_R), M_U, M_R) + A(M_U,M_R) – c(F_U)

Hence, the effect of choice variables on the probability of re-election is not different from that on the approval rate. This assumption makes the game more symmetric and easier to handle. It is also remarkable that it is relatively ‘cheaper’ for Ukraine to send troops because such a policy does not result in sanctions and the use of financial transfers is relatively more costly due to tighter budget constraints. Whether or not any country should in fact use armed forces in equilibrium is a question of Part II of this paper, which is to follow shortly.